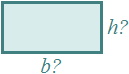Ecuaciones de primer grado
Nivel 6: 50 problemas resueltos
Introducción
Después de haber aprendido a resolver ecuaciones de primer grado en los 5 niveles anteriores, debemos ser capaces de plantear nosotros mismos las ecuaciones.
En este nivel resolvemos 50 problemas en los que tenemos que encontrar la ecuación que describe el problema y resolverla. Los temas de los problemas son, básicamente:
-
problemas de encontrar números
-
problemas de calcular edades
-
problemas de porcentajes
-
problemas de movimiento (necesitamos la fórmula \(x = v\cdot t\))
Comenzaremos con problemas sencillos y cada vez serán un poco más difíciles.
Si los 50 problemas no son suficientes:
Nota: escribimos un * en los problemas que pueden resultar más complicados.
Problema 1
Si el doble de un número más 28 es igual 82, ¿qué número es?
Solución
La incógnita \(x\) es el número que buscamos.
Como el doble se obtiene multiplicando por 2, el doble de \(x\) es \(2\cdot x\). Recordad que podemos omitir el punto: \(2x\).
El resultado de sumar 28 al doble \(x\) es 82, lo que algebraicamente se escribe como
$$ 2x + 28 = 82 $$
Resolvemos la ecuación:
$$ 2x = 82 -28 $$
$$ 2x = 54 $$
El coeficiente 2 de la incógnita pasa al otro lado dividiendo:
$$ x = \frac{54}{2} $$
Simplificamos la fracción:
$$ x = 27 $$
Por tanto, el número buscado es 27.
Problema 2
En el colegio de Miguel hay un total de 1230 estudiantes (alumnos y alumnas). Si el número de alumnas supera en 150 al número de alumnos, ¿cuántas alumnas hay en total?
Solución
La incógnita \(x\) del problema es el número total de alumnas.
Como hay 150 alumnas más que alumnos, el número de alumnos es el número de alumnas menos 150. Es decir, \(x-150\).
El número total de estudiantes es 1230 y es la suma del número de alumnas y de alumnos:
$$ x + (x-150) = 1230 $$
Hemos escrito el paréntesis para que se vea claro que es la suma del número de alumnos y del de alumnas.
Resolvemos la ecuación:
$$ x + x -150 = 1230 $$
$$ 2x -150 = 1230$$
$$ 2x = 1230+150$$
$$ 2x = 1380 $$
El 2 pasa dividiendo al otro lado:
$$ x = \frac{1380}{2} $$
$$ x = 690 $$
Por tanto, el número de alumnas es 690.
Problema 3
Si el resultado de restar el doble de \(x\) al quíntuple de \(x\) es 33, ¿qué número es \(x\)?
Solución
El quíntuple de \(x\) es \(5x\).
El doble de \(x\) es \(2x\).
Al restarle \(2x\) a \(5x\) se obtiene 33:
$$ 5x -2x = 33$$
Resolvemos la ecuación:
$$ 3x = 33 $$
El 3 pasa dividiendo al otro lado:
$$ x = \frac{33}{3} $$
$$ x = 11 $$
El número \(x\) es 11.
Problema 4
Se tiene el mismo número de cajas de manzanas que de limones. Si en una caja de manzanas caben 13 unidades y en una de limones caben 17, ¿cuántas cajas se tiene si hay un total de 180 frutas?
Solución
La incógnita \(x\) es el número de cajas de manzanas, que también es el número de cajas de limones. Entonces, el número total de cajas (de ambas frutas) es \(x+x \), es decir, \(2x\).
Como en una caja de manzanas caben 13 unidades, el número total de manzanas es \(13\cdot x\), es decir, \(13x\).
Como en una caja de limones caben 17 unidades, el número total de limones es \(17\cdot x\), es decir, \(17x\).
El total de manzanas y de limones es 180:
$$ 13x + 17x = 180 $$
Resolvemos:
$$ 30x = 180 $$
El coeficiente 30 pasa dividiendo al otro lado:
$$ x = \frac{180}{30} $$
$$ x = 6 $$
Hemos calculado el número de cajas de manzanas, pero ya hemos dicho al comienzo que el número total de cajas es \(2x\):
$$ 2x = 2\cdot 6 = 12 $$
Hay un total de 12 cajas.
Problema 5
Si la suma de un número \(x\) con su consecutivo es 27, ¿qué número es \(x\)?
Solución
Es importante saber que el consecutivo de un número se calcula sumando 1. Por ejemplo, el consecutivo de 2 es 3 (2+1 = 3) y el consecutivo de 100 es 101 (100+1 = 101).
Por tanto, el consecutivo de \(x\) es \(x+1\).
La suma de \(x\) y de \(x+1\) es igual a 27:
$$ x + (x+1) = 27 $$
Resolvemos:
$$ x +x+1 = 27 $$
$$ 2x +1 = 27 $$
$$ 2x = 27-1 $$
$$ 2x = 26 $$
$$ x = \frac{26}{2} $$
$$ x = 13 $$
Por tanto, el número \(x\) del enunciado es 13.
Problema 6
Su la suma de dos números consecutivos es -13, ¿qué números son?
Solución
La incógnita \(x\) es uno de los números que buscamos. Como el otro es su consecutivo, es \(x+1\).
La suma de los números es -13:
$$ x +(x+1) = -13 $$
$$ 2x +1 = -13 $$
$$ 2x = -13-1$$
$$ 2x = -14 $$
$$ x =\frac{-14}{2} $$
$$ x = -7 $$
Calculamos el otro número, que es \(x+1\):
$$ x+1 = -7+1 = -6 $$
Por tanto, los números consecutivos que suman -13 son -6 y -7.
Problema 7
La suma de un número par y el siguiente par que le sigue es igual a 66, ¿qué números son?
Solución
Tened en cuenta que los números naturales (0, 1, 2, 3, 4..) están ordenados y el siguiente de un número par siempre es uno impar y viceversa.
Por tanto, el número par que le sigue a otro par se calcula sumando 2. Por ejemplo, 2+2 = 4, 4+2 = 6, 6+2 = 8...
El si \(x\) es el primer número par (el pequeño), el par que le sigue es \(x+2\).
La suma de los dos números es 66:
$$ x + (x+2) = 66 $$
Resolvemos:
$$ 2x + 2 = 66 $$
$$ 2x = 66-2 $$
$$ 2x = 64 $$
$$ x = \frac{64}{2}$$
$$ x = 32 $$
Uno de los pares es 32. El otro es \(x+2\):
$$ x +2 = 32 +2 = 34 $$
Los dos pares consecutivos que suman 66 son 32 y 34.
Problema 8
Si Manuel es 3 años mayor que Andrea y la suma de sus edades es 35, ¿qué edades tienen?
Solución
Llamamos \(x\) a la edad de Andrea.
Como Manuel es 3 años mayor que Andrea, su edad es \(x+3\).
La suma de las edades es 35:
$$ x +(x+3) = 35 $$
$$ 2x +3 = 35 $$
$$ 2x = 35-3 $$
$$ 2x = 32 $$
$$ x = \frac{32}{2} $$
$$ x = 16 $$
Andrea tiene 16 años y Manuel tiene 19.
Problema 9
Si el perímetro de un cuadrado es 24cm, ¿cuánto miden sus lados?
Solución
Recordad que el perímetro de un polígono es la suma de las longitudes de sus lados.
Como un cuadrado tiene 4 lados que miden lo mismo, llamamos \(x\) a la longitud de uno de ellos.
El perímetro es la suma de los 4 lados:
$$ x+x+x+x = 24 $$
$$ 4x = 24 $$
$$ x = \frac{24}{4} $$
$$ x = 6 $$
Los lados del cuadrado miden 6cm (cada uno).
Problema 10
Calcular un número \(x\) de modo que sumar 5 al doble de \(x\) tiene el mismo resultado que restar 1 al triple de \(x\).
Solución
El doble de \(x\) es \(2x\). Le sumamos 5: \(2x + 5\).
El triple de \(x\) es \(3x\). Le restamos 1: \(3x-1\).
Los dos números anteriores tienen que ser iguales:
$$ 2x+5 = 3x-1 $$
Resolvemos la ecuación:
$$ 5 = 3x -1 -2x $$
$$ 5 = x -1 $$
$$ 5+1 = x $$
$$ 6 = x $$
El número \(x\) del problema es 6.
Problema 11
Encontrar un número de tres cifras que cumpla:
Solución
El número tiene 3 cifras. Llamamos \(x\) a la primera.
Entonces, la segunda cifra y la tercera cifra son \(2x\).
La suma de la segunda y la tercera cifra suman 12:
$$ 2x + 2x = 12 $$
$$ 4x = 12 $$
$$ x = \frac{12}{4} $$
$$ x = 3 $$
La primera cifra es 3. La segunda y la tercera cifra es \(2\cdot 3 = 6\).
Por tanto, el número de 3 cifras buscado es 366.
Problema 12
La resta de las edades de dos hermanos es 5 y la suma es 49. ¿Qué edades tienen?
Solución
Si la resta de las edades es 5 es porque uno de ellos tiene 5 años más que el otro. Así, si la edad de uno es \(x\) y la del otro es \(x+5\).
Comprobamos que la resta de las edades es 5:
$$ x+5-x = 5 $$
También sabemos que sus edades suman 49:
$$ x+(x+5) = 49 $$
$$ 2x +5 = 49 $$
$$2x = 49-5$$
$$2x = 44$$
$$ x = \frac{44}{2} $$
$$ x = 22 $$
La edad de uno es 22 y la del otro es 27.
Problema 13
Calcular tres números consecutivos que sumen 24.
Solución
El primer número es \(x\).
El consecutivo de \(x\) es \(x+1\).
El consecutivo de \(x+1\) también se calcula sumando 1:
$$ x+1 +1 = x +2$$
La suma de los tres números es 24:
$$ x+ (x+1) +(x+2) = 24 $$
Resolvemos la ecuación:
$$ 3x +3 = 24 $$
$$ 3x = 24-3 $$
$$ 3x = 21 $$
$$ x = \frac{21}{3} $$
$$ x = 7 $$
Los números son 7, 8 y 9.
Problema 14
Entre Andrés y Carla tienen un total de 42 lápices. ¿Cuántos lápices tiene Andrés si Carla tiene 6 veces más?
Solución
La incógnita \(x\) es el número de lápices que tiene Andrés.
Como Carla tiene 6 veces más que Andrés, tiene \(6x\).
En total hay 42 lápices:
$$ x + 6x = 42 $$
$$ 7x = 42 $$
$$ x = \frac{42}{7}$$
$$ x = 6 $$
Por tanto, Andrés tiene 6 lápices.
Problema 15
La edad de Javier es el triple que la de su hijo y dentro de 10 años será el doble. ¿Qué edad tiene el hijo de Javier?
Solución
La incógnita \(x\) es la edad del hijo.
Como la edad Javier es el triple que la del hijo, su edad es \(3x\).
La edad que tendrán dentro de 10 años se calcula sumando 10 a las edades actuales.
El hijo tendrá \(x+10\) y Javier tendrá \(3x+10\).
Además de esto, la edad de Javier será el doble que la de su hijo:
$$ 3x + 10 = 2\cdot (x+10) $$
Nota: es muy importante no olvidar el paréntesis para escribir el doble de la suma.
Resolvemos la ecuación:
Para eliminar el paréntesis tenemos que multiplicar por 2 sus sumandos:
$$ 3x + 10 = 2\cdot x +2\cdot 10 $$
$$ 3x + 10 = 2x + 20 $$
$$ 3x-2x = 20 -10 $$
$$ x = 10 $$
Por tanto, la edad actual del hijo de Javier es 10.
Problema 16
La suma de un número \(x\) con su mitad y con su tercera parte es igual a 22. ¿Qué número es \(x\)?
La mitad del número \(x\) es
$$ \frac{x}{2} $$
La tercera parte de \(x\) es
$$ \frac{x}{3} $$
La suma de \(x\) y de las dos fracciones es 22:
$$ x+ \frac{x}{2}+\frac{x}{3} = 22 $$
Como tenemos dos fracciones, multiplicamos la ecuación por el mcm de los denominadores (es 6):
$$ 6\cdot x + 6\cdot \frac{x}{2} + 6\cdot \frac{x}{3} =6\cdot 22 $$
Recordad que los denominadores desaparecen y quedan los numeradores multiplicados por el resultado de dividir 6 entre cada denominador:
$$ 6x+3x + 2x =132 $$
$$ 11x = 132 $$
$$ x = \frac{132}{11} $$
$$ x = 12 $$
El número \(x\) del problema es 12.
Problema 17
La mitad de un número \(x\) más la tercera parte del consecutivo de \(x\) es igual 2. Calcular \(x\).
La mitad del número \(x\) es
$$ \frac{x}{2} $$
El consecutivo de \(x\) es \(x+1\), así que su tercera parte es
$$ \frac{x+1}{3} $$
La suma de ambas fracciones es 2:
$$ \frac{x}{2} + \frac{x+1}{3} = 2$$
Multiplicamos la ecuación por el mcm de los denominadores (6):
$$ 6\cdot \frac{x}{2} + 6\cdot \frac{x+1}{3} = 6\cdot 2$$
Las fracciones desaparecen:
$$ 3x + 2\cdot (x+1) = 12 $$
No olvidéis el paréntesis para multiplicar a todo el numerador de la segunda fracción.
$$ 3x + 2x +2 = 12 $$
$$ 5x + 2 = 12$$
$$ 5x = 10 $$
$$ x = \frac{10}{5} $$
$$ x = 2 $$
El número \(x\) del problema es 2.
Problema 18
Antonio ha recorrido la quinta parte de un camino recto. Si le quedan por recorrer 520 metros, ¿cuál es la longitud del camino?
La incógnita \(x\) es la longitud total del camino.
Antonio ha recorrido la quinta parte de \(x\), es decir, ha recorrido
$$ \frac{1}{5}\cdot x $$
Nota: También podemos escribir \(\frac{x}{5}\).
Como ha recorrido la fracción 1/5 de \(x\), le quedan por recorrer las otras cuatro quintas partes de \(x\). Es decir, le queda por recorrer
$$ \frac{4}{5}\cdot x $$
Como esta fracción sabemos que es igual a 520m, tenemos la ecuación
$$ \frac{4}{5}\cdot x = 520$$
Para resolverla, pasamos el numerador dividiendo al otro lado:
$$ \frac{1}{5}\cdot x = \frac{520}{4} $$
$$ \frac{1}{5}\cdot x = 130 $$
Pasamos el denominador multiplicando:
$$ x = 130\cdot 5 $$
$$ x = 650 $$
Por tanto, la longitud del camino es 650 metros.
Problema 19
Tenemos dos garrafas de agua de la misma capacidad, pero una de ellas se encuentra al 20% y la otra al 30%. Calcular la capacidad de las garrafas si tenemos un total de 12 litros de agua.
La incógnita \(x\) es la capacidad de las garrafas.
Un porcentaje también es una fracción del total.
El 20% de \(x\) es la fracción
$$ \frac{20}{100}\cdot x $$
El 30% de \(x\) es la fracción
$$ \frac{30}{100}\cdot x $$
La suma de estas dos fracciones es 12:
$$ \frac{20}{100}\cdot x + \frac{30}{100}\cdot x = 12 $$
Multiplicamos la ecuación por 100:
$$ 20x + 30x = 1200 $$
$$ 50x = 1200 $$
$$ x = \frac{1200}{50} $$
$$ x = 24 $$
La capacidad de las botellas es de 24 litros (cada una).
Problema 20
El precio de un balón depende de su uso: el de baloncesto cuesta 10 dólares y el de fútbol cuesta 5 dólares. Si hemos comprado el mismo número de balones de cada tipo por un total de 90 dólares, ¿cuántos balones tenemos en total?
Como el número de balones de cada tipo es el mismo, lo llamamos \(x\). Entonces, el número total de balones es \(2x\).
Como tenemos \(x\) balones de baloncesto que cuestan 10 dólares cada uno, el coste total de estos balones es \(10x\).
Razonado del mismo modo, el coste total de los balones de fútbol es \(5x\).
El coste total de todos los balones es 90 dólares:
$$ 5x + 10x = 90 $$
Resolvemos la ecuación:
$$ 15x = 90 $$
$$ x = \frac{90}{15} $$
$$ x = 6 $$
Por tanto, hay 6 balones de cada tipo, así que tenemos un total de 12 balones.
Problema 21
Aurora tiene gatos y pájaros en su casa, siendo 24 el número total de sus patas. Si en total tiene 9 animales, ¿cuántos gatos tiene Aurora?
La incógnita \(x\) es el número de gatos.
Como los animales que no son gatos son pájaros, el total menos el número de gatos es el número de pájaros. Es decir, el número de pájaros que tiene Aurora es \(9-x\).
Como los gatos tienen 4 patas, suman un total de \(4x\) patas.
Como los pájaros tienen 2 patas, el total de patas de pájaros es (no olvidéis el paréntesis)
$$ 2(9-x)$$
Como el número total de patas es 24, la ecuación del problema es
$$ 4x + 2(9-x) = 24 $$
Resolvemos:
$$ 4x +18-2x = 24 $$
$$ 2x = 24-18 $$
$$ 2x = 6$$
$$ x = \frac{6}{2} $$
$$ x = 3 $$
Por tanto, Aurora tiene 3 gatos.
Problema 22
En una tienda de ropa el precio de todas las prendas es el mismo, pero a cada prenda se le aplica después un porcentaje de descuento. Nos han aplicado un 30% de descuento en una camiseta y un 10% en unos pantalones. ¿Cuál es el precio inicial de las prendas si hemos pagado en total 16€? ¿Cuánto hemos pagado por cada prenda?
La incógnita \(x\) es el precio inicial de las prendas, que sabemos que es común.
Tened en cuenta que al aplicar un 30% de descuento, pagamos el 70%. Y al aplicar un 10%, pagamos el 90%.
Por tanto, el precio final de la camiseta es
$$ \frac{70}{100}\cdot x $$
Y el precio final de los pantalones es
$$ \frac{90}{100}\cdot x $$
En total hemos pagado 16€:
$$ \frac{70}{100}\cdot x +\frac{90}{100}\cdot x =16 $$
Multiplicamos la ecuación por 100:
$$ 70x + 90x = 1600 $$
$$ 160x = 1600 $$
$$ x = \frac{1600}{160} $$
Eliminamos el cero común:
$$ x = \frac{160}{16} $$
$$ x = 10 $$
Por tanto, el precio inicial de las prendas es 10€.
Finalmente, calculamos el precio final de cada prenda:
El de la camiseta es
$$ \frac{70}{100}\cdot 10 = 7$$
Y el de los pantalones es
$$ \frac{90}{100}\cdot 10 = 9 $$
Problema 23
Pedro reparte 85 caramelos entre sus tres hijos. Al mayor le da el doble de caramelos que al menor y al mediano le da 13 caramelos más que al menor. ¿Cuántos caramelos tiene cada uno?
La incógnita \(x\) es el número de caramelos del menor.
El mayor tiene el doble de caramelos que el menor: \(2x\).
El mediano tiene 13 caramelos más que el menor: \(x+13\).
Podemos escribir una tabla con los datos:
| Mayor |
Mediano |
Menor |
Total |
| \(2x\) |
\(x+13\) |
\(x\) |
\(85\) |
El número total de caramelos es 85:
$$ x +2x +(x+13) = 85 $$
$$ 4x + 13 = 85 $$
$$ 4x = 85-13$$
$$ 4x = 72 $$
$$ x = \frac{72}{4} $$
$$ x = 18 $$
El menor tiene 18 caramelos.
El mayor tiene 36:
$$ 2x = 2\cdot 18 = 36$$
El mediano tiene 31:
$$ x+13 = 18+13=31$$
Problema 24
Sonia ha comprado unos pantalones y unos zapatos en las rebajas. Inicialmente, el precio de los zapatos era el doble que el de los pantalones, pero se ha aplicado un descuento del 10% en los pantalones y un 20% en los zapatos. En total, Sonia ha pagado \(37.5\) dólares. ¿Cuál era el precio inicial de los zapatos? ¿Y el precio final?
Nota: resolved el Problema 22 antes de resolver este.
La incógnita \(x\) es el precio inicial de los pantalones. Entonces, el precio inicial de los zapatos es \(2x\).
Al aplicar un 10% de descuento a los pantalones, su precio se queda en
$$ \frac{90}{100} \cdot x $$
Y al aplicar un 20% de descuento a los zapatos, su precio se queda en
$$ \frac{80}{100} \cdot 2x $$
Como Sonia ha pagado \(37.5\) dólares,
$$ \frac{90}{100} \cdot x+\frac{80}{100} \cdot 2x = 37.5$$
Multiplicamos la ecuación por 100:
$$ 90x + 80\cdot 2x = 3750 $$
$$ 90x + 160x = 3750 $$
$$ 250x = 3750 $$
$$ x = \frac{3750}{250} $$
$$ x = 15 $$
El precio inicial de los pantalones es 15 dólares y el de los zapatos es 30 dólares (el doble).
El precio final de los zapatos es 24 dólares:
$$ \frac{80}{100} \cdot 2\cdot 15 = 24 $$
Problema 25
En un aparcamiento hay el doble de ciclomotores (2 ruedas) que de triciclos (3 ruedas). Si la suma de las ruedas de todos los vehículos es 112, ¿cuántos vehículos hay en total?
La incógnita \(x\) es el número de triciclos. Entonces, el de ciclomotores es \(2x\). El total de vehículos es
$$ 2x +x = 3x $$
Como cada triciclo tiene 3 ruedas y hay \(x\) triciclos, el total de ruedas de triciclos es \(3x\).
Como cada ciclomotor tiene 2 ruedas y hay \(2x\) ciclomotores, el total de ruedas de ciclomotores es
$$ 2\cdot 2x = 4x $$
El número total de ruedas es 112:
$$ 3x + 4x = 112 $$
$$ 7x = 112 $$
$$ x = \frac{112}{7} $$
$$ x = 16 $$
El número de triciclos es 16 y el de ciclomotores es 32 (el doble). Por tanto, hay un total de 48 vehículos.
Problema 26
Se toma un número \(x\) y se realizan las siguientes operaciones:
-
Se suma 5 al número \(x\)
-
Se multiplica por 2 el resultado de la operación anterior
-
Se suma 5 al resultado de la operación anterior
-
Se divide entre 7 el resultado de la operación anterior
-
El resultado de la operación anterior es 5
Calcular \(x\).
-
Se suma 5 al número \(x\):
$$ x+5 $$
-
Se multiplica por 2 el resultado (no olvidéis el paréntesis):
$$ 2\cdot (x+5) $$
$$ 2x + 10 $$
-
Se suma 5 al resultado:
$$ 2x+10 + 5$$
$$ 2x + 15 $$
-
Se divide entre 7 el resultado:
$$ \frac{2x+15}{7} $$
-
El resultado es 5:
$$ \frac{2x+15}{7} = 5$$
Resolvemos la ecuación:
El 7 que divide lo pasamos multiplicando al otro lado:
$$ 2x + 15 = 35 $$
$$ 2x = 35-15$$
$$ 2x = 20 $$
$$ x = \frac{20}{2} $$
$$ x = 10 $$
El número \(x\) del problema es 10.
Problema 27
Una cuerda de 180m se corta en 3 trozos: trozo A, trozo B y trozo C. Calcular cuánto miden los trozos sabiendo que el trozo B y el trozo C miden el doble y el triple que el trozo A, respectivamente.
La incógnita \(x\) es la longitud del trozo A.
El trozo B mide el doble: \(2x\).
El trozo C mide el triple: \(3x\).
La cuerda mide 180m:
$$ x +2x +3x = 180 $$
$$ 6x = 180$$
$$ x = \frac{180}{6} $$
$$ x = 30 $$
El trozo A mide 30m, el B mide 60m y el C mide 90m.
Problema 28
Se tiene un rectángulo cuya base mide el doble que la altura. Calcular la base y la altura sabiendo que el perímetro es igual a 42m.
La incógnita \(x\) es la altura del rectángulo.
Su base mide \(2x\).
El perímetro del rectángulo es la suma del doble de la altura y del doble de la base:
$$ 2x + 2\cdot 2x = 42 $$
$$ 2x + 4x = 42 $$
$$ 6x = 42 $$
$$ x = \frac{42}{6} $$
$$ x = 7 $$
La altura mide 7m y la base mide 14m.
Problema 29
Se tiene un rectángulo cuya base mide 5 unidades más que la altura. Calcular la altura y la base del rectángulo sabiendo que su perímetro es \(54m\).
La incógnita \(x\) es la altura del triángulo.
La base mide \(x+5\).
El perímetro del rectángulo es la suma del doble de la altura y del doble de la base:
$$ 2x + 2(x+5) = 54$$
$$ 2x +2x +10 = 54 $$
$$ 4x = 54-10 $$
$$ 4x = 44 $$
$$ x = \frac{44}{4} $$
$$ x = 11 $$
La altura mide 11m y la base mide 16m.
Problema 30
El precio de la entrada de una obra de teatro es de 12 dólares y sólo se ha vendido una tercera parte de las entadas disponibles con una recaudación de 1476 dólares. ¿Cuántas entradas quedan a la venta?
La incógnita \(x\) es el número total de entradas.
El número de entradas vendidas es la tercera parte del total:
$$ \frac{x}{3} $$
Como el precio de cada entrada es de 12 dólares, el dinero recaudado con las entradas es
$$ 12\cdot \frac{x}{3}$$
Y como sabemos que la recaudación es 1476,
$$ 12\cdot \frac{x}{3} = 1476$$
Pasamos el 12 dividiendo al otro lado:
$$ \frac{x}{3} = \frac{1476}{12} $$
$$ \frac{x}{3} =123 $$
El 3 pasa multiplicando al otro lado:
$$ x = 3\cdot 123 $$
$$ x = 369 $$
El número total de entradas (vendidas y por vender) es 369. A al venta quedan \(369-123 = 246\).
¡Atención!
Problemas de velocidad
Los siguientes 3 problemas son de movimientos con velocidad constante y en línea recta. La fórmula básica de este movimiento es
$$ x = v\cdot t $$
donde \(x\) es la distancia que recorre el móvil (en \(km\)), \(v\) es la velocidad del móvil (en \(km/h\)) y \(t\) es el tiempo que dura el movimiento (en \(h\)).
Enlace: más problemas de velocidad (movimiento rectilíneo uniforme).
Problema 31
Un auto circula a una velocidad constante de \(36km/h\) durante 90 minutos (\(1.5h\)). ¿Qué distancia recorre?
La fórmula de la distancia recorrida es
$$ x = v\cdot t $$
Conocemos la velocidad y el tiempo: \(36km/h\) durante \(1.5h\).
Observad que la velocidad es kilómetros por hora y, por tanto, debemos escribir el tiempo en horas:
$$ x = 36\cdot 1.5 = 54 km $$
Problema 32
Un tren de alta velocidad tarda 45 minutos en recorrer una distancia de 240 kilómetros. ¿Cuál es su velocidad?
Escribimos el tiempo en horas para obtener la velocidad en kilómetros por hora (en lugar de kilómetros por minuto):
$$ 45 min = \frac{45}{60} h = 0.75h $$
Como \( x = v\cdot t\),
$$ 240 = v\cdot 0.75 $$
Despejamos la velocidad:
$$ v = \frac{240}{0.75} = 320 km/h$$
La velocidad del tren es \(320km/h\).
Problema 33
Si un avión vuela a velocidad de \(1040km/h\) desde Bogotá (Colombia) a Lima (Perú) y tarda 2 horas y 45 minutos, ¿cuál es la longitud de la ruta?
De la fórmula \(x = v\cdot t\) conocemos \(v\) y \(t\).
Como el tiempo es en horas y minutos, debemos escribirlo solo en horas. Los 45 minutos son
$$ 45 min = \frac{45}{60} h = 0.75 h $$
El tiempo en horas es \(2.75h\).
Sustituimos en la fórmula:
$$ x = 1040\cdot 2.75 $$
$$ x = 2860 km $$
La longitud de la ruta es 2860 kilómetros.
Problema 34
Para transportar a los 225 alumnos de un curso se emplean autobuses y autos. En cada autobús caben 50 alumnos y en cada auto, 5. Si el número de autos es 5 veces el de autobuses, ¿cuántos vehículos se emplean?
Si la incógnita \(x\) es el número de autobuses, entonces el número de autos es \(5x\).
El número total de alumnos que hay en los autos es \(5\cdot 5x\). Y en los autobuses hay \(50\cdot x\).
Como en total hay 225 alumnos,
$$ 5\cdot 5x + 50x = 225 $$
$$ 25x + 50x = 225 $$
$$ 75x = 225 $$
$$ x = \frac{225}{75} $$
$$ x = 3 $$
Se emplean 18 vehículos (3 autobuses y 15 autos).
Problema 35*
Claudia y Víctor quieren pintar una pared de \(27m^2\) entre los dos. Si Claudia tarda el doble que Víctor en pintar una misma superficie, ¿cuántos metros cuadrados pintará cada uno de ellos?
Como Claudia tarda el doble que Víctor en pintar, si Claudia pinta una superficie de \(x\) metros cuadrados, entonces Víctor pinta \(2x\).
Como la suma de las superficies que pinta cada uno debe ser el total,
$$ x + 2x = 27 $$
$$ 3x = 27 $$
$$ x = \frac{27}{3} $$
$$ x = 9 $$
Por tanto, Claudia pinta 9 metros cuadrados y Víctor pinta 18.
Problema 36*
Hace 5 años, la edad de Manuel era la quinta parte de la edad de su padre y dentro de 13 años su edad será la mitad que la de su padre. ¿Qué edad tiene Manuel actualmente?
La incógnita \(x\) es la edad actual de Manuel. Hace 5 años, su edad era \(x-5\).
Además, como hace 5 años su edad era la quinta parte que la de su padre, la edad de su padre era \(5\cdot (x-5)\).
En la actualidad, Manuel tiene \(x\) años. Y su padre tiene 5 años más de los que tenía hace 5 años:
$$ 5\cdot (x-5) + 5 $$
$$ 5x-25+5 $$
$$ 5x-20 $$
Es decir, la edad actual del padre es \(5x-20\).
Dentro de 13 años, la edad de Manuel será \(x+13\) y la de su padre será
$$ 5x -20+13$$
$$ 5x -7 $$
Además, la edad de Manuel será la mitad que la de su padre:
$$ x+13 = \frac{5x-7}{2} $$
Multiplicamos por 2 la ecuación:
$$ 2x + 26 = 5x -7$$
$$ 26 = 5x-2x-7 $$
$$ 26 = 3x-7$$
$$26+7 = 3x$$
$$ 33 = 3x $$
$$ x = \frac{33}{3} $$
$$ x = 11 $$
La edad actual de Manuel es 11.
Escribimos las edades de Manuel y de su padre en una tabla por si queréis comprobar la solución:
| Manuel |
Padre |
| 6 |
30 |
| 11 |
35 |
| 24 |
48 |
Problema 37
Se tienen tres barriles de vino de la misma capacidad, pero el nivel de vino en cada uno es distinto: el primero contiene la mitad de su capacidad, el segundo contiene cinco sextas partes de su capacidad y el tercero contiene dos terceras partes de su capacidad. Si la cantidad total de vino es 72L, ¿cuál es la capacidad de los barriles?
La incógnita \(x\) es la capacidad de los barriles.
La cantidad de agua en el primer barril es la mitad de su capacidad:
$$ \frac{1}{2}\cdot x $$
En el segundo hay cinco sextas partes de la capacidad:
$$ \frac{5}{6}\cdot x $$
En el tercero hay dos terceras partes de la capacidad:
$$ \frac{2}{3}\cdot x $$
En total hay 72L:
$$ \frac{1}{2}\cdot x + \frac{5}{6}\cdot x + \frac{2}{3}\cdot x = 72$$
Multiplicamos la ecuación por el mcm de los denominadores (6):
$$ 3x + 5x + 2\cdot 2x = 432$$
$$ 8x + 4x = 432 $$
$$ 12x = 432 $$
$$ x = \frac{432}{12} $$
$$ x = 36 $$
La capacidad de los barriles es 36L (cada uno).
Problema 38*
En casa de Lucía hay 3 cajas con la misma cantidad de bombones: caja A, caja B y caja C. Para ahorrar espacio, Lucía reparte de forma equitativa los bombones de la caja C entre las otras dos cajas. Posteriormente, Lucía se come la mitad de los bombones que hay en la caja A. Si en total quedan 27 bombones, ¿cuántos bombones había inicialmente?
La cantidad inicial de bombones en cada caja es la misma: \(x\) bombones en cada caja. Inicialmente, hay \(3x\) bombones en total.
Lucía reparte los bombones de C entre las cajas A y B (la mitad en cada uno). Por tanto, tanto en la caja A como en la B hay ahora
$$ x + \frac{x}{2} $$
Como Lucía se come la mitad de la caja A, en la caja A queda la mitad. Es decir, en A quedan
$$ \frac{1}{2}\cdot \left( x+\frac{x}{2} \right) $$
Esta cantidad más la cantidad de la caja B son los bombones que quedan:
$$ \frac{1}{2}\cdot \left( x+\frac{x}{2} \right) + x + \frac{x}{2} = 27$$
Multiplicamos por 2 la ecuación:
$$ 2\cdot \frac{1}{2}\cdot \left(x +\frac{x}{2} \right) +2\cdot x + 2\cdot\frac{x}{2} = 2\cdot 27$$
$$ x+\frac{x}{2} + 2x +x = 54 $$
$$ 4x + \frac{x}{2} = 54 $$
Multiplicamos otra vez por 2:
$$ 8x + x = 108 $$
$$ 9x = 108 $$
$$ x = \frac{108}{9} $$
$$ x = 12 $$
Por tanto, en cada caja había inicialmente 12 bombones. Como había 3 cajas, en total había 36 bombones.
Problema 39
Marta tiene 100€ para realizar una compra. Primero compra unas zapatillas y luego, con la mitad del dinero que le sobra, compra un pantalón. Si el precio del pantalón es 10€, ¿cuánto dinero le queda?
La incógnita \(x\) es el precio de las zapatillas.
Como tiene 100€ y compra las zapatillas, le quedan
$$ 100-x$$
Con la mitad de este dinero se compra un pantalón. Es decir, el precio del pantalón es
$$\frac{100-x}{2}$$
Como el precio del pantalón es 10€,
$$\frac{100-x}{2} = 10$$
Multiplicamos la ecuación por 2:
$$ 100-x = 20 $$
$$ 100-20 = x $$
$$ x = 80 $$
Marta tenía 100€ y se gasta primero 80€ y luego 10€. Por tanto, le quedan 10€.
Problema 40
Daniel se compra unas deportivas con la mitad de su dinero y con la tercera parte del dinero que le queda se compra una mochila de deporte. Si en total ha gastado 80 dólares, ¿cuánto dinero tenía inicialmente?
La incógnita \(x\) es la cantidad inicial de dinero que tenía Daniel.
Con la mitad del dinero se compra unas deportivas. Así que le queda la otra mitad:
$$ \frac{x}{2} $$
Con la tercera parte de este dinero se compra la mochila, es decir, se gasta en la mochila
$$ \frac{1}{3}\cdot \frac{x}{2} =$$
$$ =\frac{x}{6} $$
El dinero gastado en las deportivas más el gastado en la mochila es 80:
$$ \frac{x}{2} + \frac{x}{6} = 80 $$
Multiplicamos la ecuación por 6:
$$ 3x + x = 480 $$
$$ 4x = 480 $$
$$ x = \frac{480}{4} $$
$$ x = 120 $$
Daniel tenía inicialmente 120 dólares.
Problema 41
Ramón se compra unas deportivas con la tercera parte de su dinero y con la mitad del dinero que le queda se compra una camiseta. Si ha gastado un total de 40 dólares, ¿cuánto dinero tenía inicialmente?
La incógnita \(x\) es la cantidad inicial de dinero que tenía Ramón.
Ramón gasta la tercera parte del dinero con las zapatillas, es decir, gasta:
$$ \frac{x}{3} $$
Le quedan las otras dos terceras partes. Es decir, le quedan
$$ \frac{2}{3}\cdot x $$
Con la mitad del dinero que le queda se compra la camiseta, es decir, el precio de la camiseta es
$$ \frac{1}{2}\cdot \left( \frac{2}{3}\cdot x\right) =$$
$$ =\frac{2}{2\cdot 3}\cdot x $$
$$ =\frac{1}{3}\cdot x $$
$$ =\frac{x}{3}$$
El dinero que ha gastado es 40:
$$ \frac{x}{3} + \frac{1}{3}\cdot x = 40$$
Multiplicamos la ecuación por 3:
$$ x+x = 120 $$
$$ 2x = 120 $$
$$ x = \frac{120}{2} $$
$$ x = 60 $$
Ramón tenía inicialmente 60 dólares.
Problema 42
Tres hermanos se duchan todos los días a la misma hora, una detrás de otro, cuando el depósito de agua está completo. El primero consume un tercio del agua del depósito, el segundo consume la mitad del agua restante y el tercero consume toda el agua que queda en el depósito. ¿Cuál es la capacidad del depósito si los dos primeros consumen un total de 120 litros? ¿Quién consume más agua?
La incógnita \(x\) es la capacidad del depósito.
El primero consume un tercio:
$$ \frac{x}{3} $$
Después de ducharse el primero quedan dos tercios:
$$ \frac{2}{3}\cdot x $$
El segundo consume la mitad de lo que queda. Consume: $$ \frac{1}{2}\cdot \left( \frac{2}{3}\cdot x \right) =$$
$$ =\frac{x}{3} $$
Observad que queda la misma cantidad (como consume una mitad, queda la otra mitad).
Finalmente, el tercero consume el agua que quedaba:
$$ \frac{x}{3} $$
Los dos primeros consumen 120L:
$$ \frac{x}{3} + \frac{x}{3} = 120 $$
Multiplicamos por 3:
$$ x + x = 360$$
$$ 2x = 360 $$
$$ x = \frac{360}{2} $$
$$ x = 180$$
La capacidad del depósito es de 180 litros.
Observad que los tres hermanos consumen un tercio de la capacidad del depósito (\(x/3\)). Por tanto, cada uno de ellos consume 60 litros.
Problema 43*
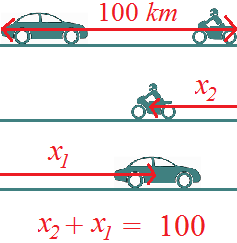
Un auto y una motocicleta circulan por la misma carretera recta, pero en sentido contrario. Ambos han partido en el mismo momento a una distancia de 100km y se quiere conocer cuánto tardarán en encontrarse.
La velocidad del auto es 120km/h y la de la motocicleta es 80km/h.
Como los dos comienzan a circular en el mismo momento, cuando se encuentren, la duración del movimiento es la misma para ambos: \(t\).
La distancia que recorre el auto en el tiempo \(t\) a una velocidad de 120km/h es
$$ x_1 = v\cdot t $$
$$ x_1 = 120\cdot t $$
La distancia que recorre la motocicleta en el tiempo \(t\) a una velocidad de 80km/h es
$$ x_2 = v\cdot t $$
$$ x_2 = 80\cdot t $$
Observad que como parten a una distancia de 100km, la suma de las distancias de los móviles debe ser igual a 100:
Es decir,
$$ x_1 + x_2 = 100$$
O lo que es lo mismo,
$$ 120\cdot t + 80 \cdot t = 100$$
Tenemos una ecuación con una incógnita (\(t\)). La resolvemos:
$$ 200t = 100$$
$$ t = \frac{100}{200} $$
$$ t = 0.5 $$
Por tanto, se encuentran en \(0.5\) horas, esto es, en 30 minutos.
Problema 44
Laura tiene caramelos de fresa, de limón y de menta. Inicialmente, tiene 5 caramelos más de limón que de fresa y 10 caramelos más de menta que de limón. Durante la semana se come todos los caramelos de fresa, la mitad de los caramelos de limón y la tercera parte de los caramelos de menta. Si ahora le quedan 30 caramelos, ¿cuántos había inicialmente?
La incógnita \(x\) es el número de caramelos de fresa.
El número de caramelos de limón es
$$ x+5 $$
Y el número de caramelos de menta es
$$ x+5+10=$$
$$ =x +15$$
Como Laura se come todos los de fresa, ya no tiene caramelos de fresa.
De limón le quedan la mitad:
$$ \frac{x+5}{2} $$
De menta la quedan dos terceras partes:
$$ \frac{2}{3}\cdot (x+15) $$
En total le quedan 30 caramelos:
$$ \frac{x+5}{2} +\frac{2}{3}\cdot (x+15) = 30$$
Multiplicamos la ecuación por el mcm de los denominadores (6):
$$ 6\cdot \frac{x+5}{2} +6\cdot \frac{2}{3}\cdot (x+15) = 6\cdot 30$$
$$ 3(x+5) + 2\cdot 2(x+15) = 180 $$
$$ 3x + 15 +4(x+15) = 180 $$
$$ 3x +15+4x+60 = 180 $$
$$ 7x + 75= 180 $$
$$7x = 180-75$$
$$ 7x = 105 $$
$$ x = \frac{105}{7} $$
$$ x = 15 $$
Inicialmente tenía 15 caramelos de fresa, 20 caramelos de limón y 30 caramelos de menta.
Por tanto, Laura tenía inicialmente 65 caramelos.
Problema 45*
Si Leonardo y Francisco tardan 1h en construir una pared con 750 ladrillos y Francisco trabaja el doble de lento que Leonardo, ¿cuánto tardarían en construir la misma pared por separado?
El número total de ladrillos es 750.
Si Francisco pone \(x\) ladrillos en 1h, Leonardo pone \(2x\) porque Francisco es el doble de rápido.
La suma de los ladrillos que ponen debe ser 750:
$$ x + 2x = 750 $$
$$ 3x = 750 $$
$$ x = \frac{750}{3}$$
$$ x = 250 $$
Por tanto, Francisco pone 250 ladrillos en 1h y Leonardo pone 500 (el doble).
Si la tarea la realizan por separado, cada uno tiene que poner 750 ladrillos.
Como Francisco pone 250 cada hora, tardará 3 horas:
$$ \frac{750}{250} = 3 $$
Como Leonardo pone 500 cada hora, tardará 1h y 30 minutos (1.5 horas):
$$ \frac{750}{500} = \frac{3}{2} = 1.5 $$
Problema 46*
Ana tarda 36 minutos en elaborar 6 pulseras de abalorios y Alba tarda 16 minutos en elaborar 4. Si tienen que realizar un encargo de 10 pulseras entre las dos, ¿cuánto tiempo tardarán?
Nota: antes de resolver este problema, haced el Problema 35 y el Problema 45.
Escribimos los datos en una tabla:
| |
Pulseras |
Minutos |
Min/pulsera |
| Ana |
6 |
36 |
6 |
| Alba |
4 |
16 |
4 |
En la tercera columna hemos escrito el tiempo medio que tarda cada una en elaborar una pulsera (se calcula dividiendo los minutos totales entre el número de pulseras).
Alba es más rápida que Ana.
¿Ana tarda el doble que Alba? No, si fuese así, tardaría 8 minutos en lugar de 6. Serían 8 porque 2·4 = 8. Es decir, en este caso, el factor por el que multiplicamos es 2.
¿Cuál es el factor \(k\) para que \(k\cdot 4 = 6\)?
Despejamos \(k\):
$$ k = \frac{6}{4} $$
Simplificamos la fracción:
$$ k = \frac{3}{2} = 1.5$$
Por tanto, en el tiempo en que Ana elabora \(x\) pulseras, Alba elabora \(1.5x\) pulseras.
En total deben elaborar 10 pulseras:
$$ x + 1.5x = 10 $$
$$ 2.5x = 10 $$
$$ x = \frac{10}{2.5} $$
$$ x = 4 $$
Por tanto, Ana elabora 4 pulseras y Alba elabora 6.
El tiempo es el mismo para ambas:
$$ 4\cdot 6 = 24 min $$
$$ 6\cdot 4 = 24min $$
Entre las dos tardan 24 minutos en elaborar las 10 pulseras.
Problema 47*
Entre Rocío y Jorge realizan una tarea en 30 minutos. Si Jorge es el doble de lento que Rocío, ¿cuánto tardan en hacer la misma tarea por separado?
Como Jorge tarda el doble que Rocío, Jorge hace una tercera parte de la tarea:
$$ \frac{1}{3} $$
Y Rocío hace dos terceras partes:
$$ \frac{2}{3} $$
Observad que la suma de las partes es el total:
$$ \frac{1}{3} +\frac{2}{3} = \frac{3}{3} = 1$$
La fracción 1 es el total.
Para calcular cuánto tarda cada uno de ellos en hacer la tarea completa aplicamos una regla de tres:
| |
Tarea |
Tiempo |
| Jorge |
1/3 |
30 |
| |
1 |
x |
Jorge tarda 90 minutos:
$$ x = \frac{1\cdot 30}{1/3} =$$
$$ = \frac{3\cdot 30}{1} =$$
$$ = 30\cdot 3 = 90 $$
| |
Tarea |
Tiempo |
| Rocío |
2/3 |
30 |
| |
1 |
x |
Rocío tarda 45 minutos:
$$ x = \frac{1\cdot 30}{2/3} = $$
$$ = \frac{3\cdot 30}{2} = 45$$
Problema 48
La edad de un antepasado de Santiago en 1944 era el triple que la que tenía en 1912. ¿En qué año nació?
La incógnita \(x\) es la edad del susodicho en el año 1912.
En el año 1944 habían pasado 32 años desde 1912 (porque 1944-1912 = 32).
Por tanto, la edad en 1944 era \(x+32\).
Se cumplió en 1944 que la edad era el triple de la edad en 1912:
$$ x+32 = 3x $$
Por tanto,
$$ x = \frac{32}{2} = 16 $$
Como en 1912 tenía 16 años, nació 16 años antes:
$$ 1912-16=1896 $$
El antepasado de Santiago nació en el año 1896.
Problema 49*
Se tienen dos números de dos cifras tales que
-
la primera cifra de ambos números es la misma
-
la segunda cifra de uno de ellos es el doble de la primera
-
la segunda cifra del otro número es el triple de la primera
-
la suma de los dos números es 75
¿Qué números son?
La incógnita \(x\) es la primera cifra de ambos números (es la misma en ambos).
La segunda cifra de uno de ellos es \(2x\) y la del otro es \(3x\).
Por tanto, los números son
$$ (x)(2x) $$
$$ (x)(3x) $$
Los paréntesis los hemos escrito para separar las cifras.
Tenemos que sumar los dos números.
Recordad que la primera cifra indica el número de decenas y la segunda el número de unidades. Por tanto, el primer número es
$$ 10\cdot x + 2x $$
El segundo es
$$ 10\cdot x + 3x $$
La suma de los números es 75:
$$ 10\cdot x + 2x + 10\cdot x + 3x = 75$$
Resolvemos la ecuación:
$$ 10x +2x +10x+3x = 75 $$
$$ 25x = 75 $$
$$ x = \frac{75}{25}$$
$$ x = 3 $$
Por tanto, los números del problema son 36 y 39:
$$ (x)(2x) = 36$$
$$ (x)(3x) = 39$$
Problema 50*
Se tiene un número de dos cifras tal que
¿Qué número es?
La incógnita \(x\) es la primera cifra del número. La segunda cifra es \(2\cdot x\). El número es
$$ (x)(2x)$$
Utilizamos los paréntesis para separar las cifras.
Cambiamos el orden de las cifras y obtenemos el número:
$$ (2x)(x)$$
Como el número \((x)(2x)\) tiene \(x\) decenas y \(2x\) unidades,
$$ (x)(2x) = 10\cdot x + 2x $$
De forma análoga,
$$ (2x)(x) = 10\cdot 2x + x $$
Sumamos los dos números:
$$ 10\cdot x + 2x + 10\cdot 2x + x = 132 $$
Resolvemos la ecuación:
$$ 10x + 2x + 20x + x = 132 $$
$$ 33x = 132 $$
$$ x = \frac{132}{33} $$
$$ x = 4 $$
Por tanto, el número buscado es 48.
Ecuaciones Resueltas ©