Teorema de Pitágoras
Problemas resueltos
Introducción
El teorema de Pitágoras proporciona la relación existente entre los catetos y la hipotenusa de un triángulo rectángulo:
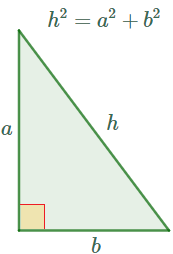
Es decir:
"El cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos."
-
La hipotenusa, \(h\), es el lado situado frente al ángulo recto (90 grados). La hipotenusa siempre mide más que los catetos.
-
Los catetos, \(a\) y \(b\), son los otros lados.
Como consecuencia del teorema, podemos obtener las siguientes fórmulas (despejando y haciendo la raíz cuadrada):
$$ h = \sqrt{a^2+b^2} $$
$$ a = \sqrt{h^2 - b^2} $$
$$ b = \sqrt{h^2 - a^2} $$
A continuación, resolvemos problemas de aplicación del teorema de Pitágoras (excepto los dos primeros, que son introductorios).
Problema 1
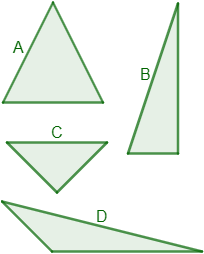
¿Cuáles de los triángulos son triángulos rectángulos?
Solución
Sólo los triángulos \(B\) y \(C\) son triángulos rectángulos. Sólo podemos aplicar el teorema de Pitágoras en estos dos triángulos.
El ángulo recto del triángulo \(B\) es el inferior derecho, el del triángulo \(C\) es el inferior.
Problema 2
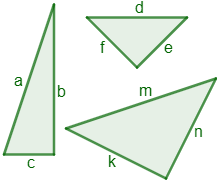
¿Cuál de los lados es la hipotenusa de los triángulos rectángulos?
Solución
Las hipotenusas de los triángulos son los lados \(a\), \(d\) y \(m\).
Problema 3
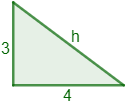
Calcular cuánto mide la hipotenusa de un triángulo rectángulo con cuyos catetos miden \(3\) y \(4\) centímetros.
Solución
Los catetos son \(a = 3\) y \(b = 4\).
Aplicamos el teorema de Pitágoras:
$$ h^2 = a^2 + b^2 $$
$$ h^2 = 3^2 + 4^2 $$
$$ h^2 = 9 + 16 $$
$$ h^2 = 25 $$
Para calcular \(h\), hacemos la raíz cuadrada:
$$ h = + \sqrt{25} $$
$$ h = 5 $$
Por tanto, la hipotenusa mide \(5\) centímetros.
Problema 4
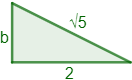
La hipotenusa de un triángulo mide \(\sqrt{5}\) y uno de sus catetos mide \(2\). ¿Cuánto mide el otro cateto?
Solución
La hipotenusa es \(h = \sqrt{5}\) y uno de los catetos es \(a = 2\).
Aplicamos el teorema de Pitágoras:
$$ h^2 = a^2 + b^2 $$
$$ (\sqrt{5})^2 = 2^2 + b^2 $$
Recordad que el cuadrado de una raíz es el valor absoluto de su radicando (lo de dentro de la raíz, pero con signo positivo), así que \((\sqrt{5})^2 = 5\).
Continuamos:
$$ 5 = 4 + b^2 $$
Pasamos el \(4\) restando al otro lado:
$$ 5-4 = b^2 $$
$$ 1 = b^2 $$
Para calcular \(b\), hacemos la raíz cuadrada:
$$ b = + \sqrt{1} $$
$$ b = 1 $$
Por tanto, el otro cateto mide \(1\).
Problema 5
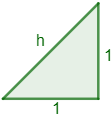
¿Cuánto mide la hipotenusa de un triángulo rectángulo cuyos catetos miden \(1\)?
Solución
Los catetos del triángulo son \(a = 1\) y \(b = 1\).
Aplicamos el teorema de Pitágoras para calcula la hipotenusa:
$$ h^2 = a^2 + b^2 $$
$$ h^2 = 1^2 + 1^2 $$
$$ h^2 = 1 + 1 $$
$$ h^2 = 2 $$
Para calcular \(h\), hacemos la raíz cuadrada:
$$ h = + \sqrt{2} $$
La hipotenusa mide \(\sqrt{2}\) (aproximadamente, \(1{,}41\)).
Problema 6
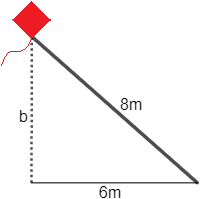
¿A qué altura está la cometa de Ana si su cuerda mide \(L = 8\) metros y tendría que moverse \(6\) metros para situarse debajo de ella?
Solución
El ángulo que forma la altura con el suelo es un ángulo recto, con lo que tenemos un triángulo rectángulo.
La cuerda es la hipotenusa del triángulo: \(h = 8\).
La distancia que habría que desplazarse es la base del triángulo, es decir, uno de los catetos: \(a = 6\).
La altura a la que se encuentra la cometa es el otro cateto: \(b\).
Aplicamos el teorema de Pitágoras:
$$ h^2 = a^2 + b^2 $$
$$ 8^2 = 6^2 + b^2 $$
$$ 64 = 36 + b^2 $$
Pasamos \(36\) al otro lado:
$$ 64-36 = b^2 $$
$$ 28 = b^2 $$
Para calcular \(b\), hacemos la raíz cuadrada:
$$ b = + \sqrt{28} $$
Podemos escribir el número \(28\) como un producto para simplificar:
$$ b = \sqrt{7·2·2} $$
Como hay un \(2^2\), sale de la raíz un \(2\):
$$ b = 2\sqrt{7} $$
Se encuentra a \(2\sqrt{7}\) metros de altura (aproximadamente, \(5{,}29 \ m\)).
Problema 7
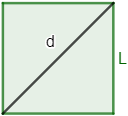
¿Cuánto miden los lados de un cuadrado cuya diagonal mide \(d = 2\)?
Solución
Un cuadrado está formado por dos triángulos rectángulos iguales. La diagonal del cuadrado, \(d\), es la hipotenusa de los triángulos.
Como se trata de un cuadrado, sus cuatro lados miden lo mismo, \(L\). Así, los catetos de los triángulos también miden \(L\).
Aplicamos el teorema de Pitágoras:
$$ d^2 = L^2 + L^2 $$
$$ 2^2 = L^2 + L^2 $$
$$ 4 = 2·L^2 $$
Pasamos el \(2\) dividiendo al otro lado:
$$ \frac{4}{2} = L^2 $$
$$ 2 = L^2 $$
Hacemos la raíz cuadrada:
$$ L = +\sqrt{2} $$
Por tanto, los lados del cuadrado miden \(\sqrt{2}\) (aproximadamente, \(1{,}41\)).
Problema 8
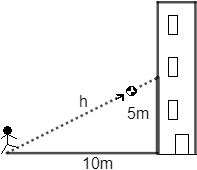
Jaime está a \(10\) metros de un edificio y lanza su balón en línea recta ascendente y alcanza el segundo piso del edificio (\(5\) metros de altura). ¿Cuánto mide la trayectoria del balón (desde que lanza hasta que impacta)?
Solución
La trayectoria del balón es la hipotenusa de un triángulo rectángulo con catetos \(a = 5\) y \(b = 10\).
Aplicamos el teorema de Pitágoras para calcular la hipotenusa, \(h\):
$$ h^2 = a^2 + b^2 $$
$$ h^2 = 5^2 + 10^2 $$
$$ h^2 = 25+100 $$
$$ h^2 = 125 $$
Hacemos la raíz cuadrada:
$$ h = +\sqrt{125} $$
$$ h =\sqrt{5·5·5} $$
$$ h = 5\sqrt{5} $$
La trayectoria del balón mide \(5\sqrt{5}\) metros (aproximadamente, \(11{,}18\)).
Problema 9
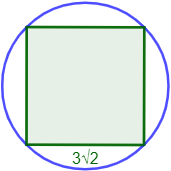
Calcular el radio de una circunferencia que tiene inscrito un cuadrado de lado \(L = 3\sqrt{2}\).
Solución
Por un lado, el diámetro es el doble del radio de la circunferencia.
Por otro, el diámetro coincide con la diagonal del cuadrado:
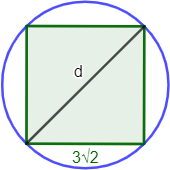
Por tanto, el radio es la mitad de la diagonal del cuadrado.
La diagonal del cuadrado, \(d\), la podemos calcular aplicando el teorema de Pitágoras:
$$ d^2 = L^2 + L^2 $$
$$ d^2 = 2L^2 $$
$$ d^2 = 2·(3\sqrt{2})^2 $$
Tenemos que calcular la potencia de un producto, que es el producto de las potencias:
$$(3\sqrt{2})^2 = 3^2 ·(\sqrt{2})^2 =$$
$$ = 9·2 = 18 $$
Por tanto,
$$ d^2 = 2·18 $$
$$ d^2 = 36 $$
Haciendo la raíz cuadrada, tenemos la diagonal:
$$ d = +\sqrt{36} $$
$$ d = 6$$
Calculamos el radio de la circunferencia (la mitad del diámetro):
$$ r = \frac{6}{2} = 3$$
Problema 10
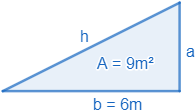
Calcular la hipotenusa de un triángulo rectángulo de base \(b=6\ m\) y área \(A = 9\ m^2\).
Solución
El área de un triángulo es la mitad de la base, \(b\), por la altura, \(a\):
$$ A = \frac{b\cdot a}{2} $$
Como el área es \(9\) y base mide \(6\), tenemos
$$ 9 = \frac{6\cdot a}{2} $$
Resolvemos la ecuación:
$$ 9 = \frac{6\cdot a}{2} $$
$$ 9·2 = 6\cdot a $$
$$ 18 = 6·a $$
$$ a = \frac{18}{6} = 3 $$
Por tanto, la altura mide \(3\) metros.
Como la base y la altura son los catetos del triángulo, podemos calcular cuánto mide la hipotenusa por el teorema de Pitágoras:
$$ h^2 = a^2 + b^2 $$
$$ h^2 = 3^2 + 6^2 $$
$$ h^2 = 9 + 36 = 45 $$
$$ h = +\sqrt{45} $$
$$ h = +\sqrt{3·3·5} $$
$$ h = 3·\sqrt{5} $$
Por tanto, la hipotenusa del triángulo mide \(3\sqrt{5}\) metros (aproximadamente, \(6{,}7\)).
Problema para pensar
En un triángulo rectángulo, ¿alguno de los catetos puede medir más que la hipotenusa? Razonar la respuesta.
Solución
La hipotenusa siempre mide más que los catetos.
Supongamos que el cateto \(a\) mide más que la hipotenusa \(h\): \(a > h\). En este caso, el cuadrado del cateto mide más que el de la hipotenusa: \( a^2 > h^2\). Por ejemplo, \(3> 2\) y \(3^2 = 9 > 4 = 2^2\).
Por el teorema de Pitágoras, el cuadrado de la hipotenusa, \(h\), es
$$ h^2 = a^2 + b^2 $$
Despejando, el cuadrado del cateto \(b\) es
$$ b^2 = h^2 - a^2 $$
Como hemos visto que \(a^2\) es mayor que \(h^2\), entonces, la resta \(h^2-a^2\) es negativa:
$$ b^2 = h^2 - a^2 < 0$$
Como consecuencia, el cuadrado de \(b\) también es negativo, lo cual es imposible porque un cuadrado no puede ser negativo. Esto es absurdo.
Es decir, si suponemos que un cateto mide más que la hipotenusa, llegamos a un absurdo. Por tanto, esta hipótesis es falsa.
Veamos un ejemplo: supongamos un triángulo rectángulo cuya hipotenusa mide 2 y uno de sus catetos mide 3. Aplicamos Pitágoras para calcular el otro cateto, \(b\):
$$ h^2 = a^2 +b^2 $$
$$ 2^2 = 3^2+b^2 $$
$$ 4 = 9 +b^2 $$
$$ b^2 = 4-9 $$
$$ b^2 = -5 $$
$$ b = \sqrt{-5} $$